For whatever reason, this week felt particularly long. While most states are seeing an increase in the number of COVID-19 cases there is very little movement to limit the spread of the disease with anything beyond mask orders and polite requests to maintain social distancing. There’s a lot of numbers and information being shared around about COVID-19 and I wanted to add some context to that by simulating a small gathering of friends.
To do this experiment I’ll be using dice to simulate the odds of different things when it comes to COVID-19. For the odds I’ll be using some rough, not as scientific estimates to make the math a little easier. Numbers are vaguely taken from known cases worldwide according to the Johns Hopkins dataset along with a paper to define asymptomatic, and an estimate for spread during house parties based on one in Connecticut [link, link, link].
- Percent positive of guests after a party: 50%
- Percent with COVID-19 that are asymptomatic: 45%
- Percent with COVID-19 that have mild symptoms: 35%
- Percent with COVID-19 that need hospitalization: 15%
- Percent with COVID-19 that die: 5%
With that known, let’s have our get together! It’s been a long quarantine and no one has yet had any symptoms of COVID-19, so a couple invites their neighborhood game store friends over as everyone is long overdue for a lazy afternoon of board games.
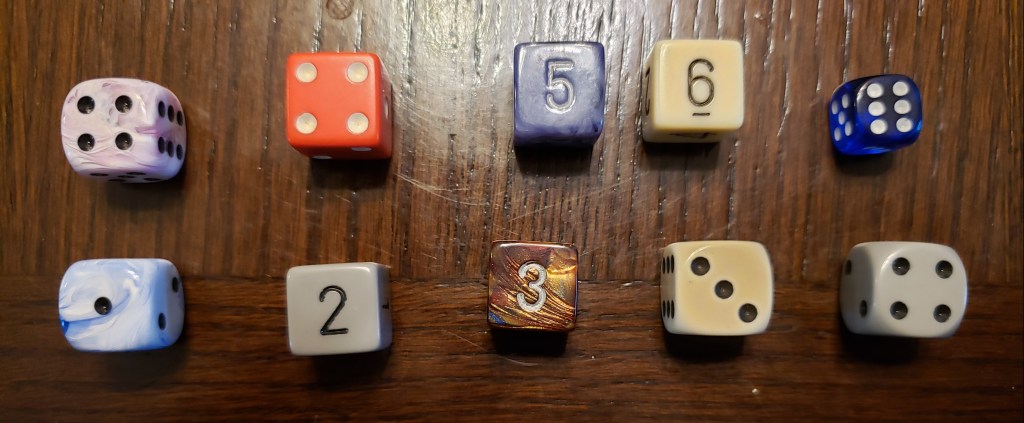
The 1 – Male in his 30’s
The 2 – Woman in her 40’s
The 3’s – Men in their 30’s
The 4’s – Parents in their 40’s; 18 year old son
The 5 – Male in his 30’s
The 6’s – Couple in 60’s
The party starts and while people are at first very careful of all of the appropriate measures, they just can’t maintain it after everyone decides the risk of exposure is minimal as no one is sick or had any direct contact with someone who is sick. Different people rotate through several short games and the 3’s and 4’s break out an old favorite and play several rounds. Food is eaten, drink is had, and there is plenty of merriment for all. Mr 5 sneezes a few times which at first has a people jumping, but once everyone remembers his allergies to the 3’s cat Bunny everyone relaxes and laughs it off. For a short time it doesn’t feel like the COVID-19 world anymore, it just feels like life. The party comes to a close as the sun sets and people return to their COVID lives.
Ms. 2 begins coughing a few days later and while her temperature starts out low enough, the cough worsens she feels like she can never catch her breath while developing a fever of 102F. Terrified she phones her doctor who giver her a location to get tested at. With all her strength for a single day she drives to a testing site, gets her brain prodded through her nose on each side, and goes home to sleep and wait. It’s now been a week since the party and her test results are back, she cries when she looks at the phone… Results: Positive
The party was all indoors with everyone spending several hours with each other, sometimes arguing fiercely over rules or cheering a win. Ms. 2 texts everyone and tells them to get tested for COVID-19 immediately. There’s not a lot of data on just how many people get sick at a long indoor function, but the odds here are 50/50. The dice are rolled, 1-3 means no illness and 4-6 means they have COVID-19. Each die represents the same person from the previous image, but now the number displayed determines if they caught COVID-19 or not.

Half of the party becomes ill after catching COVID-19 from Ms. 2. Some of the people at this point have symptoms by the time while others will develop them during the next week if at all. For those who became ill, there’s a further roll of the dice based on the ratios stated at the beginning. Due to the prevalence of COVID-19 and what the data is based on I’ll be using a 20 sided die to represent the range of outcomes, but anyone who rolls a 1 will succumb to the disease.
- Outcomes are as follows:
- 12 and over – Asymptomatic
- 5-11 – Home care
- 2-4 – Hospitalization
- 1 – Death
Sometimes there’s nothing we can do and a healthy, young person succumbs to the disease, Mr. 3 passes.

For those that survive, their outcomes are influenced by their characteristics, here simplified to age and gender. There has been a recent Nature publication that looked into the hazard ratio for a variety of characteristics and their possible influence on COVID-19 outcomes. Hazard Ratios (HR) run on a scale with 1.00 as the base where a number larger than 1 shows an increase in risk and a number lower than one shows a decrease in risk [link].
I’ll be using the HR fully adjusted values in Table 2 and translate them into multipliers for the dice. Numbers higher than one will decrease the adjusted number while numbers lower than one will increase the adjusted number. The only reason I’m doing this is to reflect the influence of characteristics on the numbers rolled, this is not the real way to interpret HR!
- HR 0.06 – multiply rolled number by 8
- HR 0.30 – multiply rolled number by 4
- HR 1.59 – divide rolled number by 1.5
- HR 2.50 – divide rolled number by 2.5

I’ve labeled the dice first by their initial number and characteristics, then their hazard ratios, their initial twenty sided die roll, and finally their adjusted 20 sided die roll. This is all meant to reflect that each individual characteristic can impact the outcome of their COVID-19 case.
An adult in their 40’s can go from a roll of 3 to have a better outcome than expected due to the benefit of their age while an older adult in their 60’s can have an initial roll of 6 and wind up hospitalized. This only becomes more complicated to predict with more characteristics included such as smoking status, weight, and even race.
COVID-19 is so devastating because it’s about odds. Those odds, like the hazard ratios and outcomes, are based on available data which can be difficult to get depending on the location. Less data means there are more assumptions which can decrease accuracy. Reporting of thorough, truthful data helps everyone keep a better eye on their community and helps scientists make better calculations.
Recognize your risks, and identify the ones you’re willing to take.
Until next time,
Your friendly neighborhood scientist
